Art

Spirograph: The Beauty of Mathematics

Dhairya Bhardwaj

Dhairya Bhardwaj

— 5 min read

This post is an archive of my old blog, which I no longer maintain!

Welcome back! In the previous post The beauty of Mathematics you got to see the awesomeness of mathematics illustrated using programming in python. This post augments the series.

While experimenting with the Turtle Graphics, I was in search of some more whimsical patterns. I wanted to draw a cardioid but I was unable to do in the beginning. While searching for the solution, I came to know about an old school tool: Spirograph on this site. The designs created by this tool was too fascinating to make me include them in my art gallery .

Let’s have a quick look on the these fantastic patterns 😉

Do you find them interesting? I guess your answer is none other than yes! But the question is how to implement them and how it’s all related to the mathematics? No worries! I am here to explain the implementation so that you can start experimenting with the Spirograph (or just try it!)

Before moving forward check off the following checklist:

  1. Visit The previous blog post: The beauty of Mathematics
  2. Know how to code in Python 3.
  3. Know how to use Turtle Graphics in Python 3
  4. Read about Spirograph, Hypotrochoid, Epitrochoids

Now you are sorted! Let’s start!

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#import dependencies
import turtle
from random import randint
from math import sin,cos,degrees,radians
 
 
#intial setup
scr=turtle.Screen() #Screen Intialization, opens up a window
scr.clearscreen() #clears the screen
scr.tracer(0,0) #makes the turtle works faster (doesn't animate every step)
tobj=turtle.Turtle() #intializes a turtle on the screen opened
tobj.hideturtle() #hides the turtle pointer
 
 
 
#important functions
def gotoxy(t:turtle.Turtle,x,y):
    '''moves the turtle to (x,y) position without drawing anything'''
    t.penup()
    t.setposition(x,y)
    t.pendown()
     
random256 = lambda:  randint(0,255)
colorstring=lambda: '#%02X%02X%02X' % (random256(),random256(),random256())
# colorsting() generates a hex string for a random color

Once you are done with initial setup, let’s try implementing the following equations:

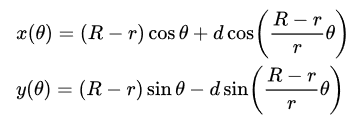
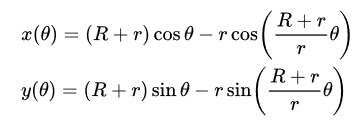
Parametric equation of Hypotrochoid
Parametric equation of Epitrochoid

you can play around with these equation interactively here (you must try this tool).
As you can see, the above functions are trigonometric and hence periodic. We must know the time-period to ensure that we draw a complete cycle of a Hypotrochoid/Epitrochoid. This helped me to find out the number of 360° rounds that the smaller circle (one with radius r) takes to draw the complete pattern.
if r/R-r (or r/R+r) is simplified to a fraction ( rational number ) as b/a (or b:a) then 2bπ is the time-period for the above functions or we can say b is the number of rounds. Now you can look at the implementation.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
def drawparametric(t:turtle.Turtle,xθ,yθ,rounds):
    '''
    enter the parametric equations (as function of theta) x(θ) and y(θ)
    it is utility for drawing spirograph
    '''
    theta=0
    step=5 #the length of equally spaced small intervals, (or say dθ)
    while theta <= rounds*360:
        if theta is 0:
            t.penup()
        y = yθ(theta)
        x = xθ(theta)
        t.setpos(x,y)
        if theta is 0:
            t.pendown()
        theta+=step
     
 
def hypertrochoid(t:turtle.Turtle,R,r,d):
    k= lambda theta: (R-r)*radians(theta)/r
    xtheta= lambda theta: (R-r)*cos(radians(theta))+d*cos(k(theta))
    ytheta= lambda theta: (R-r)*sin(radians(theta))-d*sin(k(theta))
    rounds = Fraction(r/(R-r)).limit_denominator(100).numerator
    drawparametric(t,xtheta,ytheta,rounds)
 
def Epitrochoid(t:turtle.Turtle,R,r,d):
    k= lambda theta: (R+r)*radians(theta)/r
    xtheta= lambda theta: (R+r)*cos(radians(theta))-d*cos(k(theta))
    ytheta= lambda theta: (R+r)*sin(radians(theta))-d*sin(k(theta))
    rounds = Fraction(r/(R+r)).limit_denominator(100).numerator
    drawparametric(t,xtheta,ytheta,rounds)
 
#try running Fraction(11,10) without limiting the denominator will give you the logic behind using limit denominator

Now you are all set to draw your first design. 🙂

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
tobj.speed(0) # Sets the speed of turtle, Remark:  0 sets the speed heighest
tobj.color(colorstring(),colorstring()) # Sets the line colour and fill colours (randomly).
tobj.begin_fill()
Epitrochoid(tobj,90,70,40)
tobj.end_fill()
tobj.color(colorstring(),colorstring())
tobj.begin_fill()
hypertrochoid(tobj,90,20,10)
tobj.end_fill()
tobj.color(colorstring(),colorstring())
tobj.begin_fill()
Epitrochoid(tobj,40,9,5)
tobj.end_fill()
tobj.color(colorstring(),colorstring())
tobj.begin_fill()
hypertrochoid(tobj,50,35,34)
tobj.end_fill()
scr.update()

The above code draws the following design

Cool! isn’t it? 😉
Go ahead and start experimenting with your program . And remember, it’s not about the language you use, it’s all about the logic, mathematics and your dedication . 🙂

TODO: the centre is (0,0) for the above functions. Try translating the origin.

For more pictures and future updates, visit my Art Gallery.
I hope you enjoyed the journey. leave your experience/queries below in the comments. Signing out.

Read more